What Is Fibonacci Sequence?

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding numbers. The sequence starts with 0 and 1, and each subsequent number is calculated by adding the two previous numbers together. In mathematical terms, the Fibonacci sequence is defined as:

F(0) = 0 F(1) = 1 F(n) = F(n-1) + F(n-2) for n > 1

So, the Fibonacci sequence begins as follows: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

Naive Solution Using Recursion

The Fibonacci Sequence is recursive in nature where each number is the addition of the previous two numbers. It can be solved using recursion.

Let's say, we want to create a Fibonacci sequence until 6.

We have a starting point where we know about the first two numbers of the Fibonacci sequence which are 0 and 1. Then we can start from 2 and start calculating the Fibonacci sequence until n (n is 6 for this example).

Formula : f(n) = f(n-1) + f(n-2)

f(0) = 0 , f(1) = 1

f(2) = f(1) + f(0) = 0 + 1 = 1

f(3) = f(2) + f(1) = 1 + 1 = 2

f(4) = f(3) + f(2) = 2 + 1 = 3

f(5) = f(4) + f(3) = 3 + 2 = 5

f(6) = f(5) + f(4) = 5 + 3 = 8

So, the answer to the Fibonacci sequence until 6 is 8.

Recursion Tree Diagram

Here is a recursion tree to understand all recursion calls while solving the Fibonacci sequence of number 6.

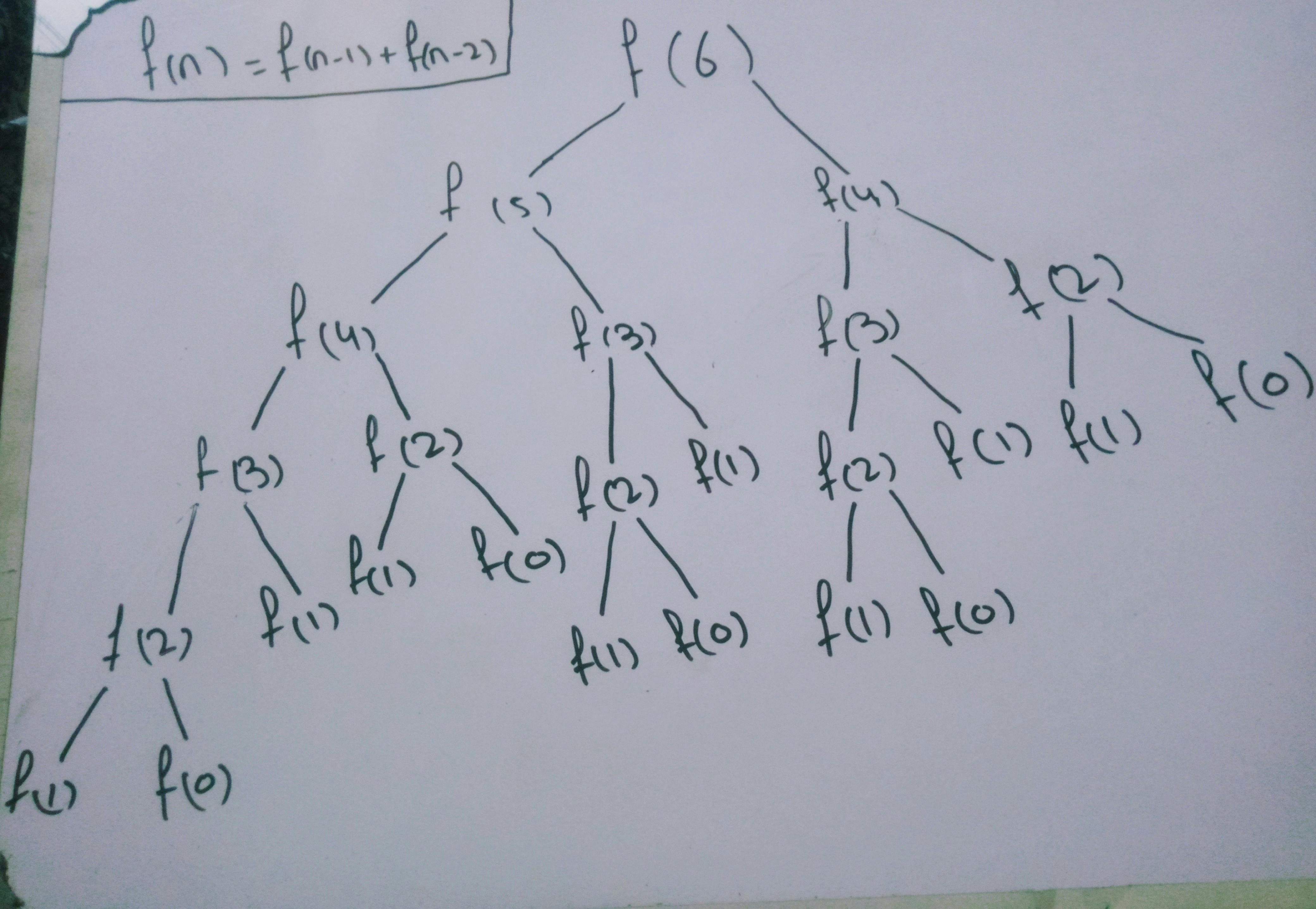
Code For Recursive Solution

def f(n):
    if n <= 1:
        return n # if n = 0, return 0, if n = 1 return 1
    return f(n-1) + f(n-2)
f(6) # Returns 8

Time And Space Complexity For Recursive Solution

The time complexity for the above given recursive solution is O(2^n). The time complexity is O(2^n) because at each level of the recursion tree, we have two options or two branches and we have a maximum of n levels in the recursion tree. That's why the time complexity is O(n^2). We can improve this time complexity using dynamic programming.

The space complexity for the above-mentioned recursive solution will be O(n) because the maximum of n recursion calls is stored in the stack at a time.

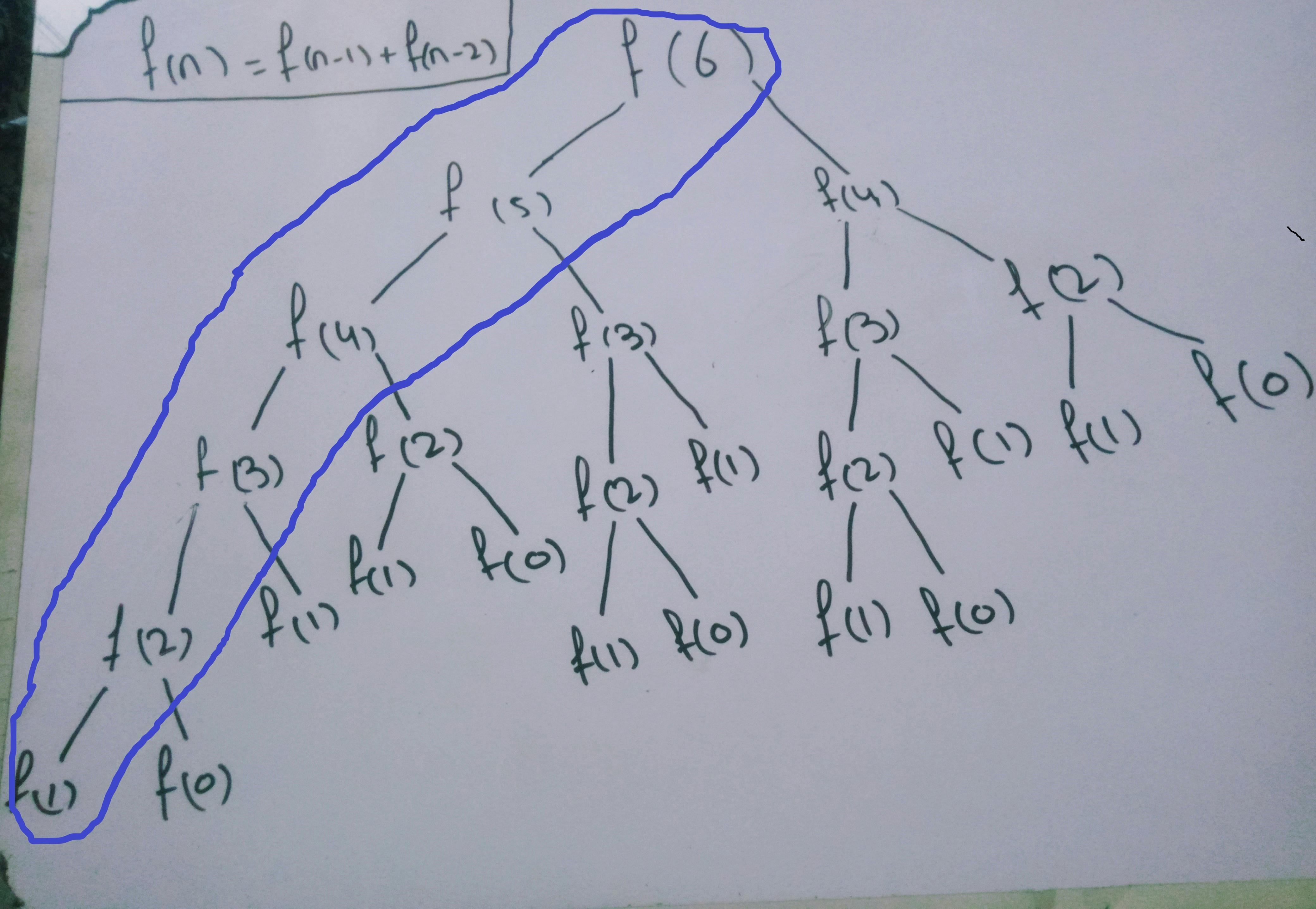
Problem in Recursive Solution

The main problem in the recursive solution is that we have repetitive recursion calls as you can see in the above diagram. The recursive function is calling again and again for f(2),f(3), and f(4) for different recursion calls. The one thing that came to mind is why we are calculating the same function with the same input again and again. Can we optimize it? If we could not optimize this solution then it will be very time-consuming to calculate the Fibonacci sequence for large numbers like 50 or 100 because there will be a lot of repetitive function calls.

Dynamic Programming

The key idea behind dynamic programming is to solve each subproblem only once and store its solution for future reference. This approach avoids redundant calculations and improves the overall efficiency of the algorithm.

We will apply dynamic programming specifically a top-down approach to the above given recursive solution of the Fibonacci sequence to optimize it.

The main idea behind using dynamic programming in this problem is that we will calculate the Fibonacci sequence of some number like f(2) and then store this number with the return answer in some data structure like a hashmap or array. When we will again need to calculate the Fibonacci sequence of f(2), then instead of calculating the Fibonacci sequence of f(2) again, we will just get the output of the f(2) Fibonacci sequence from the data structure.

This technique of storing the output of the recursive call in the data structure is called memoization.

Recursion Tree Diagram for Optimized Solution Using Dynamic Programming

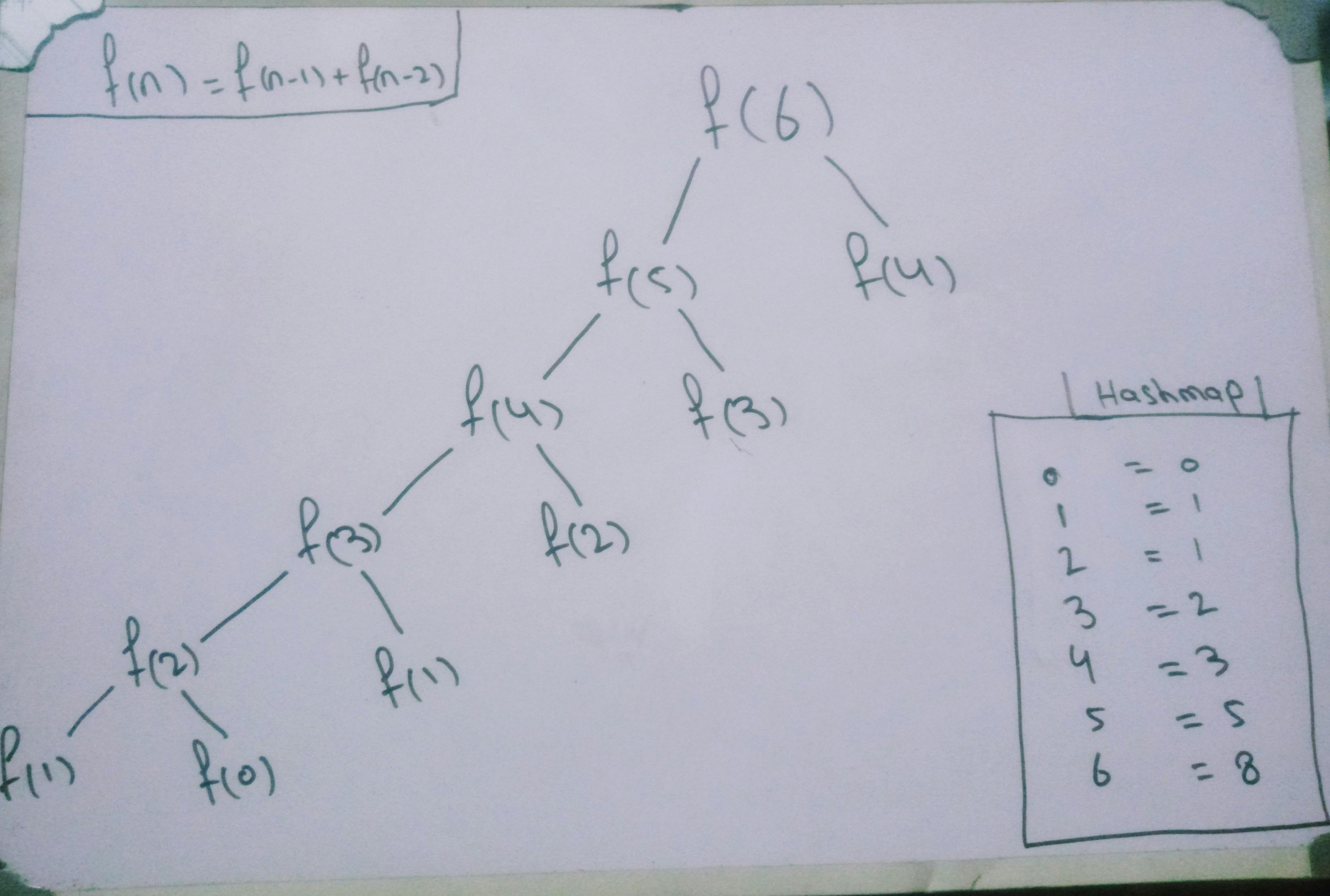
Code For Dynamic Programming Implementation

def f(n,cache):
    if n in cache:
        return cache[n] # if n found in cache, then return value of n from cache .No need to calculate furthur.
    if n <= 1:
        cache[n] = n
        return cache[n]
    cache[n] = f(n-1,cache) + f(n-2,cache) # storing the recursion call ouput in cache for later use.
    return cache[n] # Return cache[n] , the value of n that we have stored in the cache in the above line.

Breakdown Of Dynamic Programming Solution

Let's use a hashmap data structure to store the output of recursive calls. At the start, the hashmap will be empty.

cache = {} # Hashmap

• First of all, we will call the Fibonacci function by passing the number 6. The function will keep running until it reached the base condition which is f(n) <= 1.

• For f(0), the function will return 0 and then we will memoize this function call by storing the number 0 as the key and the output of the function which is also 0 as the value in the cache.

• cache = { 0 : 0 }

• For f(1), the function will return 1 and then we will memoize this function call by storing the number 1 as the key and the output of the function which is also 1 as the value in the cache.

• cache = { 0 : 0, 1 : 1}

• For f(2), the function will return 1 and then we will memoize this function call by storing the number 2 as the key and the output of the function which is 1 as the value in the cache.

• cache = { 0 : 0, 1 : 1, 2 : 1}

• Now, In any other recursive call, if we will need to calculate the f(0),f(1) or f(2), we will simply check in the cache if this function is already calculated or not. If the n will present in the cache then we will return the value of the n instead of recalculating the function again for that n.

• This will help to optimize the recursive solution of the Fibonacci sequence using the memoization technique of dynamic programming.

• Similarly, the output of the other recursion calls will be stored in the cache and the final cache output will look like this.

• cache = { 0 : 0, 1 : 1, 2 : 1, 3 : 2, 4 : 3, 5 : 5, 6 : 8 }

Time And Space Complexity For the Dynamic Programming Solution

The time complexity of the dynamic programming solution with memoization for the Fibonacci sequence is O(n), where n is the input value.

This is because, in the worst case, the function needs to compute and store the Fibonacci numbers from 0 up to n once. Each Fibonacci number is computed only once and then stored in the memoization dictionary, which can be looked up in O(1) time for subsequent calls.

As for space complexity, it is also O(n). The memoization dictionary cache grows proportionally with the input value n. It stores the computed Fibonacci numbers, with each number requiring constant space. Therefore, the space complexity is linear with respect to the input value.

I hope you have understood the dynamic programming implementation of the Fibonacci Sequence. I have tried to explain it to the best of my knowledge but if you find any mistakes or you have any suggestions to improve this article, then feel free to share your message in the comments.

Regards, Arslan Haroon

#Programming #DSA #DynamicProgramming #Recursion